Graph - Laplacian Matrix

 

Laplacian Matrix

• 정의 :
  $$L = D - A$$
  $D$는 노드의 차수를 나타내는 대각 행렬 각 대각 원소 $D_{ii}$는 노드 $i$의 차수
  $A$는 그래프의 인접 행렬
  
  
• 금융 네트워크에서의 활용
  • 커뮤니티 구조 식별
    라플라시안 행렬은 금융 네트워크 내의 클러스터 또는 커뮤니티를 식별하는 데 사용될 수 있다
  • 위험 관리
    라플라시안 행렬의 고유값과 고유벡터를 분석하여, 네트워크에 중요한 노드를 식별하고, 해당 노드의 실패가 네트워크에 미치는 영향을 평가할 수 있다.

---

Signed Laplacian Matrix

• 정의 
  $$L_{\text{signed}} = D - A_{\text{signed}}$$
  
  
• 금융 네트워크에서의 활용
  • 신뢰/불신 네트워크 분석
    신뢰 네트워크에서는 양수 엣지가 높은 신뢰도를 나타내고, 음수 엣지가 높은 리스크나 불신을 나타내므로, 이를 통해 네트워크의 전반적인 리스크를 평가할 수 있다.
    기업들 간의 신뢰 관계는 긍정적인 협력 관계로, 불신 관계는 경쟁 관계로 볼 수 있다. Signed Laplacian Matrix를 사용하여 다음과 같은 분석을 수행할 수 있다
    - 네트워크 내에서 신뢰 관계가 강한 부분을 식별하고, 이 부분이 네트워크의 안정성에 미치는 영향을 평가
    - 불신 관계가 집중된 부분을 식별하고, 이러한 관계가 전체 네트워크의 리스크에 어떻게 영향을 미치는지 평가
    - 신뢰/불신 관계를 기반으로 커뮤니티를 식별하여, 금융 네트워크 내에서 협력적 또는 경쟁적 집단을 분석
• 예시
  $$A_{\text{signed}} = \begin{bmatrix} 0 & 1 & -1 & 0 \\ 1 & 0 & 1 & -1 \\ -1 & 1 & 0 & 1 \\ 0 & -1 & 1 & 0 \end{bmatrix}$$ $$D = \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix}$$ $$L_{\text{signed}} = D - A_{\text{signed}} = \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix} - \begin{bmatrix} 0 & 1 & -1 & 0 \\ 1 & 0 & 1 & -1 \\ -1 & 1 & 0 & 1 \\ 0 & -1 & 1 & 0 \end{bmatrix} = \begin{bmatrix} 2 & -1 & 1 & 0 \\ -1 & 3 & -1 & 1 \\ 1 & -1 & 3 & -1 \\ 0 & 1 & -1 & 2 \end{bmatrix}$$

---

Symmetric Normalized Laplacian

• 정의:
  $$L_{\text{sym}} = I - D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$$
  
  • 대각 원소 ($L_{\text{sym}}[i, i]$): 항상 1이다.
    이는 노드가 자신과의 관계를 나타내며, 자기 자신과의 정규화된 연결 강도는 항상 1로 유지된다.
  • 비대각 원소 ($L_{\text{sym}}[i, j]$, $i \neq j$)
    인접 노드 간의 관계를 나타내며, 정규화된 값으로 표현된다. 이는 노드의 연결 강도를 균형 있게 반영한다.
• 금융 네트워크에서의 활용
  • 정규화된 영향 분석
    각 노드의 영향력을 정규화하여 비교할 수 있다. 이는 다양한 크기의 주체들이 있는 네트워크에서 중요하다.
  • 스펙트럴 클러스터링
    스펙트럴 클러스터링에 사용되어, 금융 네트워크 내의 유사한 행동을 보이는 주체들을 식별할 수 있다.
• 예시
  $$A = \begin{bmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{bmatrix}$$ $$D = \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix}$$ $$D^{-\frac{1}{2}} = \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{3}} & 0 \\ 0 & 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix}$$ $$D^{-\frac{1}{2}} A D^{-\frac{1}{\sqrt{2}}} = \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{3}} & 0 \\ 0 & 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{3}} & 0 \\ 0 & 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} 0 & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & 0 \\ \frac{1}{\sqrt{6}} & 0 & \frac{1}{3} & \frac{1}{3\sqrt{2}} \\ \frac{1}{\sqrt{6}} & \frac{1}{3} & 0 & \frac{1}{3\sqrt{2}} \\ 0 & \frac{1}{3\sqrt{2}} & \frac{1}{3\sqrt{2}} & 0 \end{bmatrix}$$ $$L_{\text{sym}} = I - D^{-\frac{1}{2}} A D^{-\frac{1}{2}} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} - \begin{bmatrix} 0 & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & 0 \\ \frac{1}{\sqrt{6}} & 0 & \frac{1}{3} & \frac{1}{3\sqrt{2}} \\ \frac{1}{\sqrt{6}} & \frac{1}{3} & 0 & \frac{1}{3\sqrt{2}} \\ 0 & \frac{1}{3\sqrt{2}} & \frac{1}{3\sqrt{2}} & 0 \end{bmatrix} = \begin{bmatrix} 1 & -\frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{6}} & 0 \\ -\frac{1}{\sqrt{6}} & 1 & -\frac{1}{3} & -\frac{1}{3\sqrt{2}} \\ -\frac{1}{\sqrt{6}} & -\frac{1}{3} & 1 & -\frac{1}{3\sqrt{2}} \\ 0 & -\frac{1}{3\sqrt{2}} & -\frac{1}{3\sqrt{2}} & 1 \end{bmatrix}$$

---

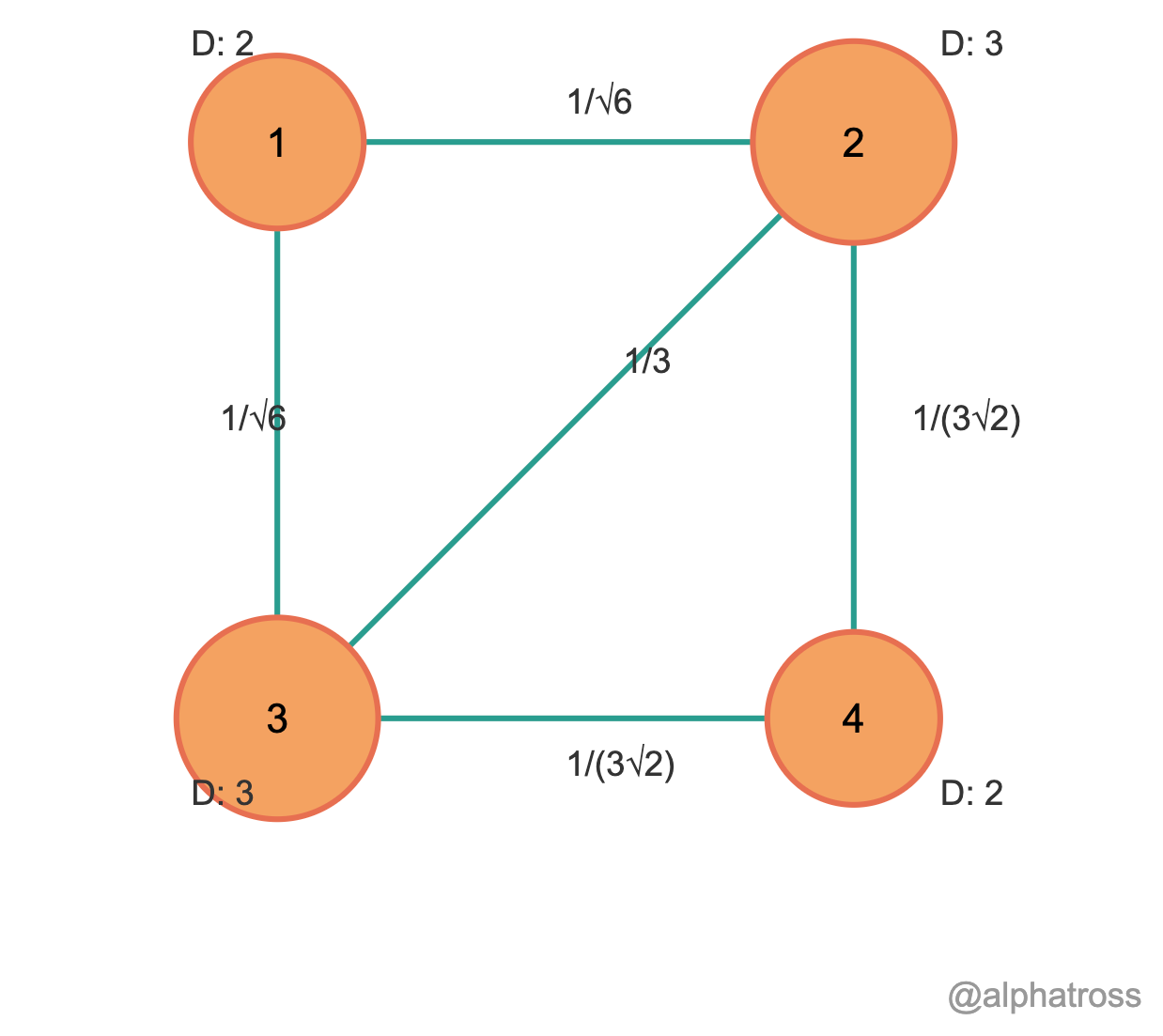
Random Walk Normalized Laplacian

• 정의
  $$L_{\text{rw}} = I - D^{-1} A$$
  
  • 대각 원소 ($L_{\text{rw}}[i, i]$) : 항상 1이다. 
  • 비대각 원소 ($L_{\text{rw}}[i, j]$, $i \neq j$) : 인접 노드 간의 관계를 나타내며, 정규화된 값으로 표현된다.
• 금융 네트워크에서의 활용:
  • 확산 과정 모델링
    금융 네트워크 내에서의 정보나 충격의 확산 과정을 모델링할 수 있다.
  • 랜덤 워크 기반 분석
    랜덤 워크 프로세스를 통해 네트워크 내에서 특정 노드의 중요성을 평가하거나, 자산의 상관 관계를 분석할 수 있다.
• 예시
  $$A = \begin{bmatrix}  0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{bmatrix}$$ $$D = \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix}$$ $$D^{-1} = \begin{bmatrix} \frac{1}{2} & 0 & 0 & 0 \\ 0 & \frac{1}{3} & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 \\ 0 & 0 & 0 & \frac{1}{2} \end{bmatrix}$$ $$D^{-1} A = \begin{bmatrix} \frac{1}{2} & 0 & 0 & 0 \\ 0 & \frac{1}{3} & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 \\ 0 & 0 & 0 & \frac{1}{2} \end{bmatrix} \begin{bmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & \frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{3} & 0 & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{3} & \frac{1}{3} & 0 & \frac{1}{3} \\ 0 & \frac{1}{2} & \frac{1}{2} & 0 \end{bmatrix}$$ $$L_{\text{rw}} = I - D^{-1} A = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} - \begin{bmatrix} 0 & \frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{3} & 0 & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{3} & \frac{1}{3} & 0 & \frac{1}{3} \\ 0 & \frac{1}{2} & \frac{1}{2} & 0 \end{bmatrix} = \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} & 0 \\ -\frac{1}{3} & 1 & -\frac{1}{3} & -\frac{1}{3} \\ -\frac{1}{3} & -\frac{1}{3} & 1 & -\frac{1}{3} \\ 0 & -\frac{1}{2} & -\frac{1}{2} & 1 \end{bmatrix}$$

---

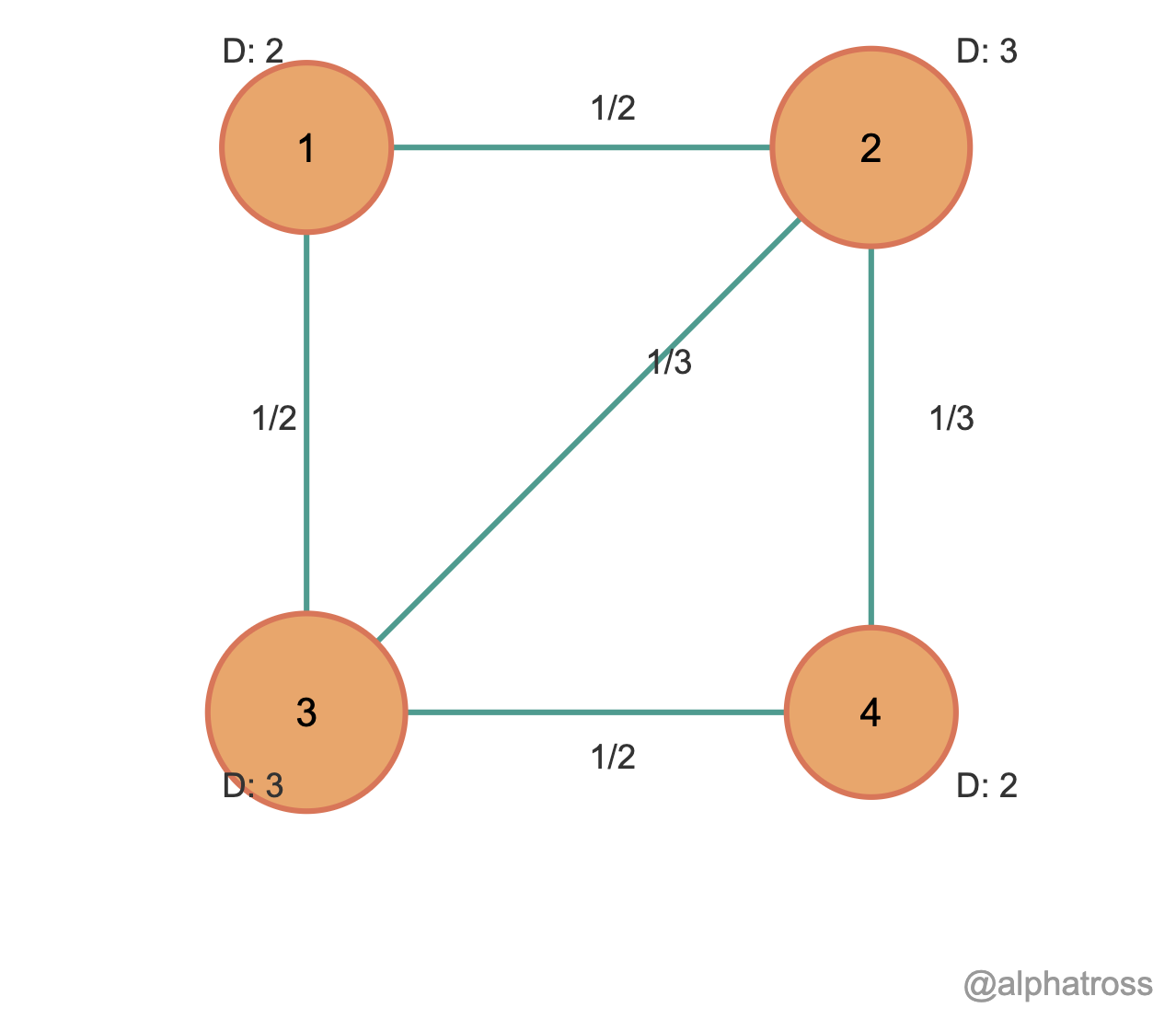
Symmetric Normalized Laplacian 와 Random Walk Normalized Laplacian 의 차이점 비교

 

두 라플라시안은 서로 다른 방식으로 그래프 구조를 표현하며, 각각의 장단점이 있다. $L_sym$은 그래프의 전체적인 구조를 분석하는 데 더 적합하고, $L_rw$는 노드 간의 전이 확률을 직접적으로 표현하여 확산 과정을 모델링하는 데 더 유용하다. 사용 목적과 분석하고자 하는 그래프의 특성에 따라 적절한 라플라시안을 선택하는 것이 중요하다.

1. 대칭성
   $L_{\text{sym}}$은 대칭 행렬 이는 행렬의 고유값이 모두 실수이며, 고유벡터가 직교한다는 의미이다
   $L_{\text{rw}}$는 일반적으로 비대칭 행렬 이는 행렬의 고유값이 실수 또는 복소수일 수 있음을 의미한다
   
   
2. 고유값 & 고유벡터
   $L_{\text{sym}}$고유값이 [0, 2] 구간에 위치하며, 작은 고유값은 그래프의 클러스터 구조를 반영한다.
   $L_{\text{rw}}$ 고유값이 [0, 1] 구간에 위치하며, 작은 고유값은 느린 확산 과정을 반영한다
   $L_{\text{sym}}$과 $L_{\text{rw}}$는 같은 고유값을 가진다. 이는 두 행렬이 스펙트럼 특성을 공유함을 의미한다.
   $L_{\text{sym}}$의 고유벡터 $v$와 $L_{\text{rw}}$의 고유벡터 $u$ 사이에는 $u = D^(1/2)v$ 관계가 있다.
   
   
3. 해석
   $L_sym$: 노드의 차수에 따라 양방향으로 정규화된다. 이는 무방향 그래프의 구조를 잘 보존한다
   $L_rw$: 랜덤 워크의 전이 확률을 직접 나타낸다. 각 행의 합이 0이 되어, 확률 해석이 용이하다
   
   
4. 그래프 표현:
   $L_sym$: 엣지의 가중치가 양 끝 노드의 차수에 의해 정규화된다.
   $L_rw$: 엣지의 가중치가 출발 노드의 차수에 의해서만 정규화된다.
   
   
5.  응용:
   $L_sym$ 은스펙트럴 클러스터링에 주로 사용되며, 그래프의 전체적인 구조를 분석하는 데 유용하다.
    $L_rw$는 랜덤 워크 관점에서 그래프 내에서 정보나 충격이 확산되는 과정을 모델링. 이는 네트워크에서 노드의 중요도와 연결성을 평가하는 데 유용하다
    $L_rw$는  구글의 페이지랭크 알고리즘에서 사용하는 행렬은 랜덤 워크 정규화 라플라시안과 유사하다 웹 페이지 간의 링크 구조를 모델링하여 페이지의 중요도를 평가한다.