| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 틱데이터
- 틱
- 금융딥러닝
- 아비트라지랩 #arbitragelab #아비트라지 #arbitrage #residual #reversion #residualreverstion #hudsonthames #허드슨
- AFML
- 금융머신러닝
- 테슬라 #tesla #ai #퀀트
- >
- 실전 금융 머신 러닝 완벽 분석
- Today
- Total
알파트로스
[HudsonThames 리딩그룹] Robust Detection of Lead-Lag Relationships in Lagged Multi-Factor Models (1) 본문
[HudsonThames 리딩그룹] Robust Detection of Lead-Lag Relationships in Lagged Multi-Factor Models (1)
알파트로스 2024. 6. 22. 22:13
괴리를 이용한 전략에 사용해 보고자 한다.
Price Dicovery
다중 시계열은 시스템을 이해하는 데 중요한 정보를 제공한다. 이러한 시스템에는 시간이 지남에 따라 변화하는 여러가지 상호 연관된 변수가 포함되는 경우가 많다. 하지만 개별 시계열에 대한 분석만으로는 이러한 변수 간 상호작용과 의존성을 완전히 이해하기 어렵다.
Lead-Lag Relationships는 두 시계열 간의 time-shifted dependence를 의미한다. 이 관계를 탐구하면 예측이나 군집화 등의 다양한 분야에서 유용한 통찰을 얻을 수 있다. 하지만 고차원 시계열 데이터에서 Lead-Lag Relationships를 탐지하는 것은 도전 과제이다. 전통적인 방법론은 데이터의 노이즈나 이질성에 영향을 받거나 미묘한 의존성을 적절히 반영하지 못할 수 있다.

이 논문에서는 Multi-factor models에서 Lead-Lag Relationships를 강건하게 탐지하기 위해 클러스터 인터뷰 방법론을 제안한다. 이 방법론은 통해 복잡한 다변량 시계열 시스템에서 Lead-Lag Relationships를 식별하고 분석하는 데 따르는 어려움을 극복하고자 한다. 저자들은 Sliding Window 접근법을 사용하여 각 시계열에서 subsequences 시계열을 생성하고, subsequences 시계열로 이루어진 큰 유니버스를 만든다. 이 단계에서 데이터 내의 모든 잠재적인 Lead-Lag Relationships 고려할 수 있게 된다. 다음으로, k-means++, 스펙트럼 클러스터링과 같은 다양한 클러스터링 기법을 적용하여 추출된 시계열을 그룹화한다. 이때 비선형성까지도 고려하는 여러 다른 pairwise similarity를 활용하기도 한다.
(TODO)클러스터가 시간적으로 정렬되면 작성자는 클러스터 간에 지연된 추정치를 조정합니다. 이 프로세스는 지역 시계열의 일관된 관계에 대한 조사를 강화하여 데이터에 존재하는 리드-래그 역학에 대한 보다 신뢰할 수 있고 포괄적인 이해를 제공합니다. 저자들은 또한 여기서 반드시 언급하지는 않겠지만, 모프 다중 참조 정렬 문제와도 연관성을 설정합니다. 하지만 이 문제도 후속 시계열을 서로 이동시켜 노이즈를 포착하는 문제와 관련이 있으므로 원하신다면 읽어보시기 바랍니다.
Once the clusters have been aligned in time, the authors will adjust the lagged estimates across clusters. This aggregation process enhances their investigation of consistent relationships in the regional universe of time series, providing a more reliable and comprehensive understanding of the lead-lag dynamics present in the data. The authors also establish connections to the Morphe multi-reference alignment problem,
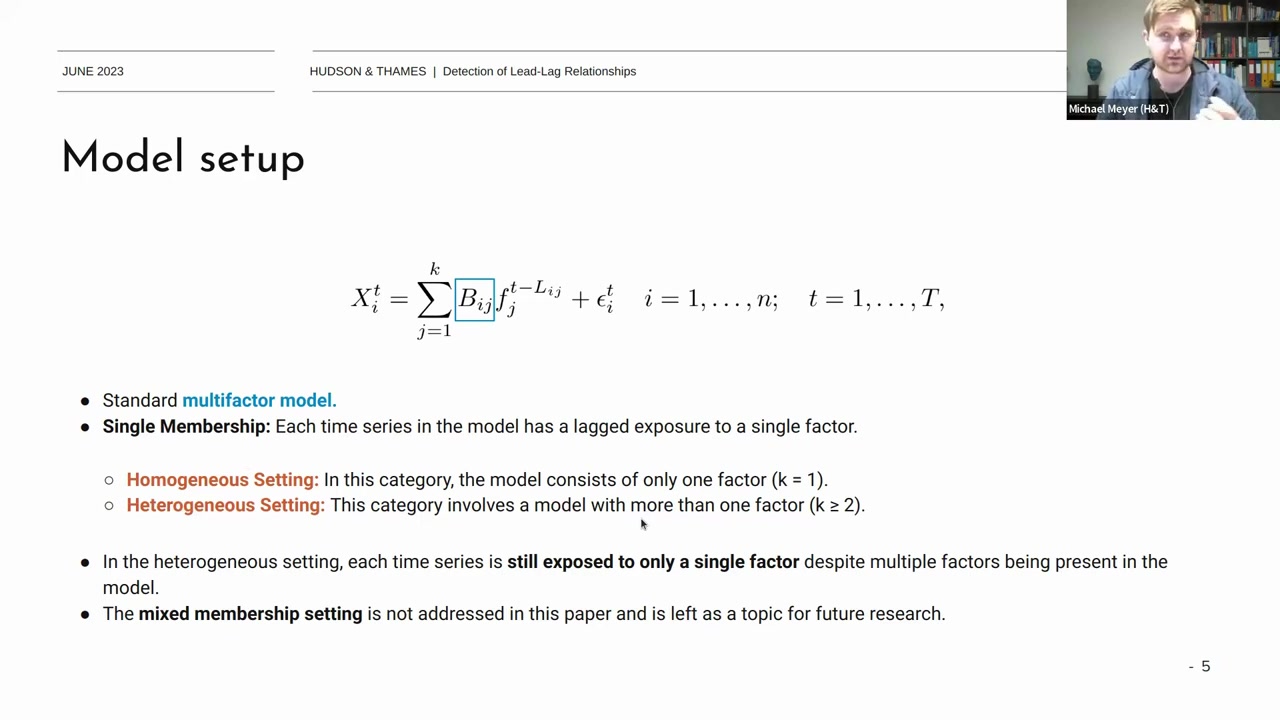
이 논문에서는 일반적인 multi factor model을 사용한다.
\[ X^t_i = \sum_{j=1}^{k} B_{ij} f^{t-L_{ij}}_j + \epsilon^t_i \]
- \( X^t_i \) : 시간 \( t \)에서 시계열 \( i \)의 값
- \( k \) : factor의 수
- \( B_{ij} \) : 시계열 \( i \)가 factor \( j \)에 노출된 정도
- \( f^{t-L_{ij}}_j \) : 시간 \( t \)에서 요인 \( j \)의 값에 대한 lag
- \( \epsilon^t_i \) : 잔차
Single membership
이 모델은 각 시계열이 단일 factor에 lagged된 노출을(= single membership) 갖는다. 이 설정에는 두 가지 변형이 있다.
- homogeneous setting: 모델이 단일 factor(K=1)만 포함된다
- heterogeneous setting: 모델에 여러 factor(K>2)가 포함되지만 각 시계열은 여전히 단일 factor에 노출된다.
Mixed membership setting 은 이 논문에서 다루지 않으며, 미래 연구 주제로 남겨둔다.
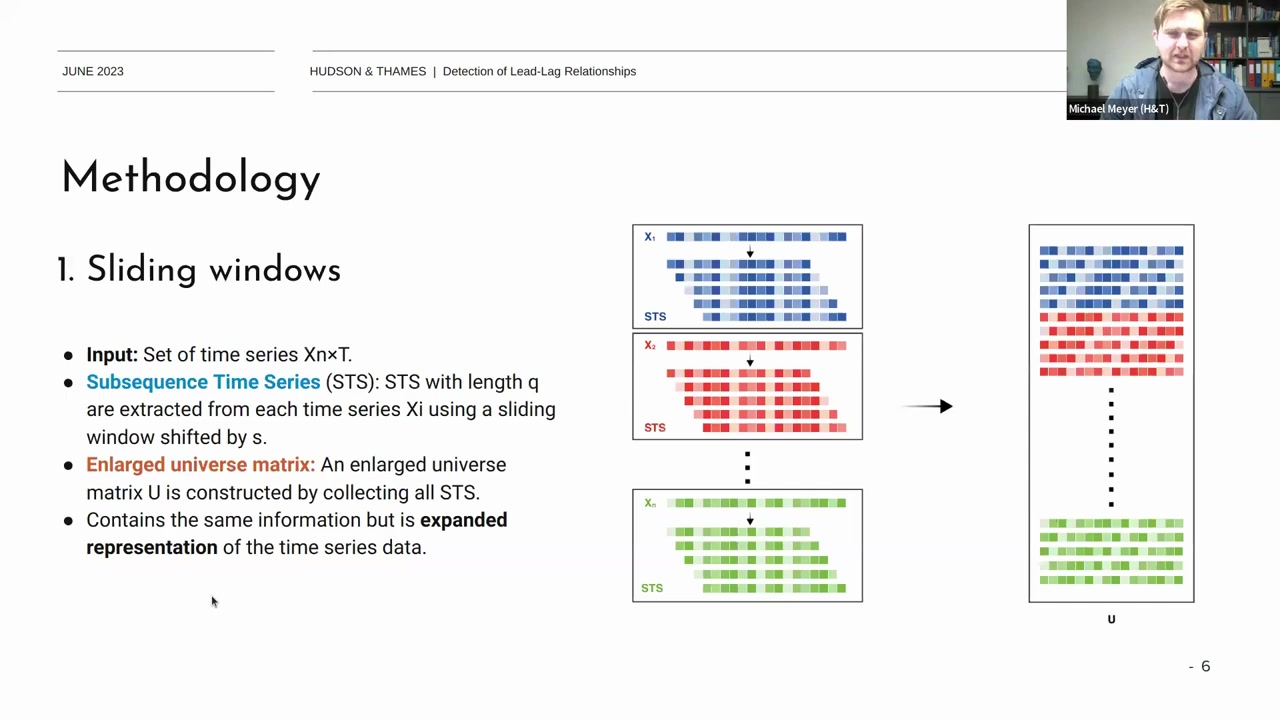
Input
- 시간 시계열 데이터 \(X_{n \times T}\) 세트.
Subsequence Time Series (STS)
- \(X_i \) 시계열 데이터에서 길이 \(q\) 인 subsequence 를 추출.
- 슬라이딩 윈도우 기법으로 각 시계열 \(X_i \) 를 시프트 \(s\) 만큼 이동하여 subsequence 시계열 생성.
- 예를 들어, \(X_i \)에서 길이 \(q\) 인 STS를 생성하고, 이 과정을 모든 시계열 \(X_1, X_2, \ldots, X_n\) 에 적용
Enlarged Universe Matrix (U):
- 각 시계열에서 추출한 subsequence 시계열을 하나의 큰 행렬 U로 결합.
- 이 행렬 U는 각 시계열의 subsequence를 포함하며, 원래 시계열 데이터를 확장하여 표현.
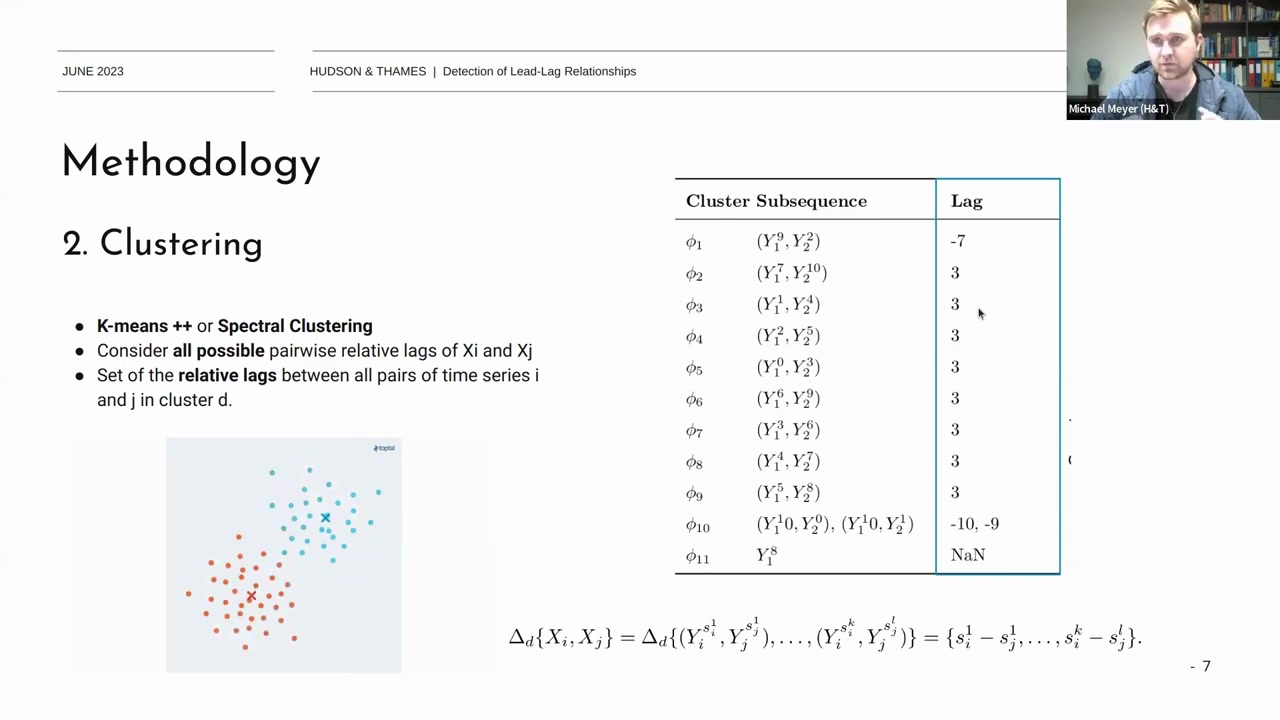
Clustering:
- 여기서 사용하는 방법론은 K-means 또는 Spectral Clustering이다. 대부분의 결과는 K-means를 기반으로 하며, 나중에 Spectrum Clustering에 대한 심층 분석도 포함된다
Covariance Matrix와 Distance Matrix:
- 모든 시계열 데이터를 covariance matrix로 변환한 후, 이를 distance matrix로 변환합니다. 논문에서는 정확히 이 과정을 설명하지 않지만, 일반적으로 최적의 클러스터 수를 결정하기 위해 사용하는 방법론 유사할 것이다.
Optimal Number of Clusters:
- 클러스터의 최적 개수를 결정하기 위해, 여러 클러스터를 시도해보고 최적의 개수를 결정한다. K-means++는 다음 중심점을 선택할 때 이전 중심점으로부터의 거리를 고려하여 좀 더 효과적으로 클러스터링을 수행한다
Set of Relative Lags:
\(\Delta_d \{ X_i, X_j \} = \Delta_d \{ (Y_i^{s_1}, Y_j^{s_1}), \ldots, (Y_i^{s_k}, Y_j^{s_k}) \} = \{ s_i^1 - s_j^1, \ldots, s_i^k - s_j^k \}\)
- 클러스터 d내에 존재하는 모든 가능한 시계열 pair \(X_i\)와 \(X_j\)사이의 relative lags 의 집합.
- 예를 들어 \(Y_i^{s_1}, Y_j^{s_1}\)은 \(X_i\)와 \(X_j\)의 첫번째 subsequence pair 이고 relative lags는 각 subsequence 쌍에서 \(s_i^k\)와 \(s_j^k\)의 차이를 계산하여 구한다
- 시계열 \(X_i\)와 \(X_j\)가 있고, 각 시계열의 길이가 T=100, subsequence 길이가 q=10, sliding window의 이동 간격이 s=1라고 가정할때 각 시계열의 subsequence 수는 다음과 같이 계산된다:
\(k = \left\lfloor \frac{100 - 10}{1} \right\rfloor + 1 = 91\) - 따라서 가능한 subsequence 쌍의 수는 k×k=91×91=8281 따라서, 두 시계열 간의 모든 가능한 subsequence 쌍의 상대적 시차는 8281개의 값을 가지게 된다
\(\Delta_d \{ X_i, X_j \} = \{ s_i^1 - s_j^1, s_i^1 - s_j^2, \ldots, s_i^{91} - s_j^{91} \} \)
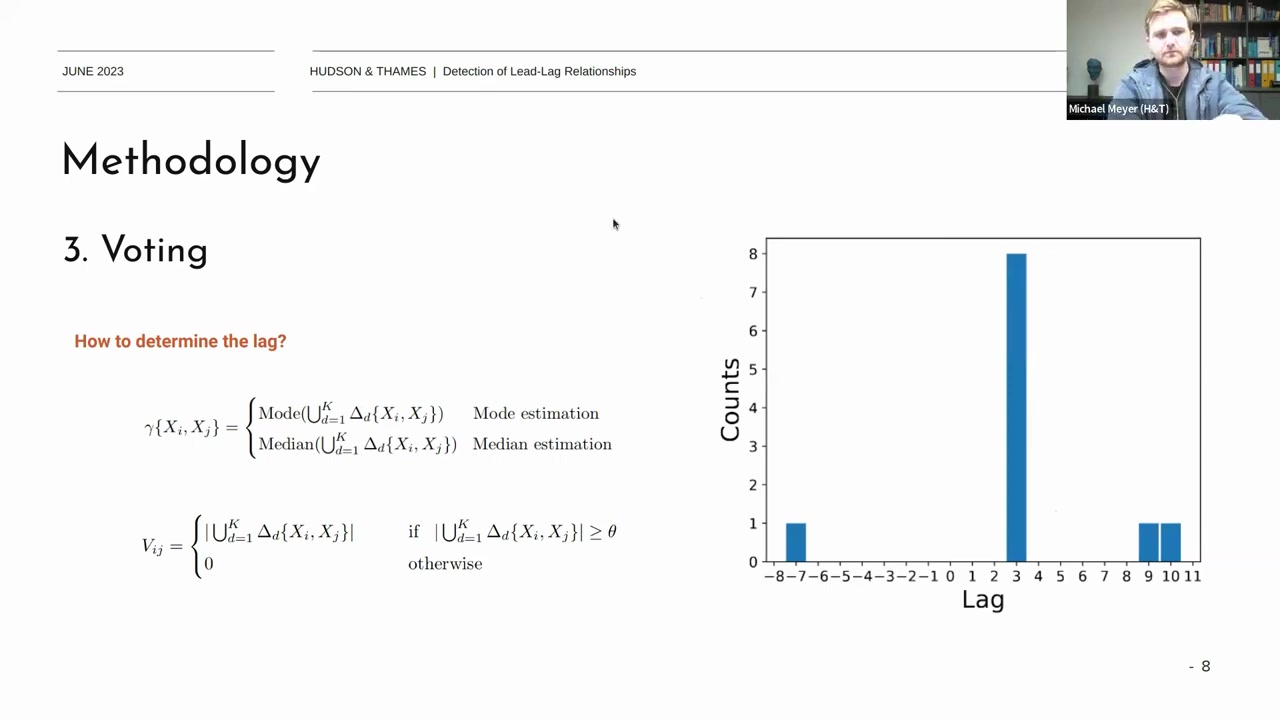
Determine Lead-Lag Relationship:
- 클러스터 내의 모든 시계열 pair과 그 시차를 분석하여 자주 발생하는 시차를 기반으로 lead-lag 관계를 결정한다. 일반적으로 모드(mode)나 중간값(median)을 사용하여 가장 자주 발생하는 시차를 선택한다.
- 알고리즘의 개선된 부분은 동일한 클러스터에서 \(X_i\)와\(X_j\)사이의 subsequence 시계열의 시차 수를 합산하여 투표 행렬을 계산하는 것입니다. 그런 다음 문서에서 정의된 \(\theta\) 라는 투표 임계값을 설정하여 작은 수의 개수를 필터링합니다.
- 이 방식은 subsequence 시계열이 일관되게 여러 클러스터에서 함께 클러스터되지 않는 한, 결과적으로 얻어진 시차 추정값이 정확하지 않을 가능성이 높다는 점에 착안했다

- 생성데이터를 활용한 실험은 두 가지 설정, 즉 Homogeneous Setting과 Heterogeneous Setting으로 나누어 진행된다 Homogeneous Setting에서는 모든 자산이 동일한 시차 및 노출을 가지므로 비교적 단순합니다. Heterogeneous Setting 에서는 자산마다 다른 시차 및 노출을 가지므로 더 복잡합니다. 시계열 데이터를 시뮬레이션하고, 각 설정에 따라 요인 노출과 시차를 분석합니다.
- \(M = 5\) : 최대 시차
- \(T=100\): 시간 단계 수
- \(n=6\): 자산의 수
- \(q=90\): 시계열의 길이
- Homogeneous Setting:
- 모든 자산이 동일한 시차 및 노출을 가집니다.
- 예를 들어, 모든 자산이 시차 0, 1, 2, 3, 4, 5에서 동일하게 노출됩니다.
- Heterogeneous Setting:
- 자산마다 다른 시차 및 노출을 가집니다.
- 예를 들어, 시계열 1, 2, 3은 요인 1에 노출되고, 시계열 4, 5, 6은 요인 2에 노출됩니다.
- 시차도 다르게 적용됩니다. 예를 들어, 시계열 1은 시차 0에서 노출되고, 시계열 2는 시차 2에서 노출됩니다.
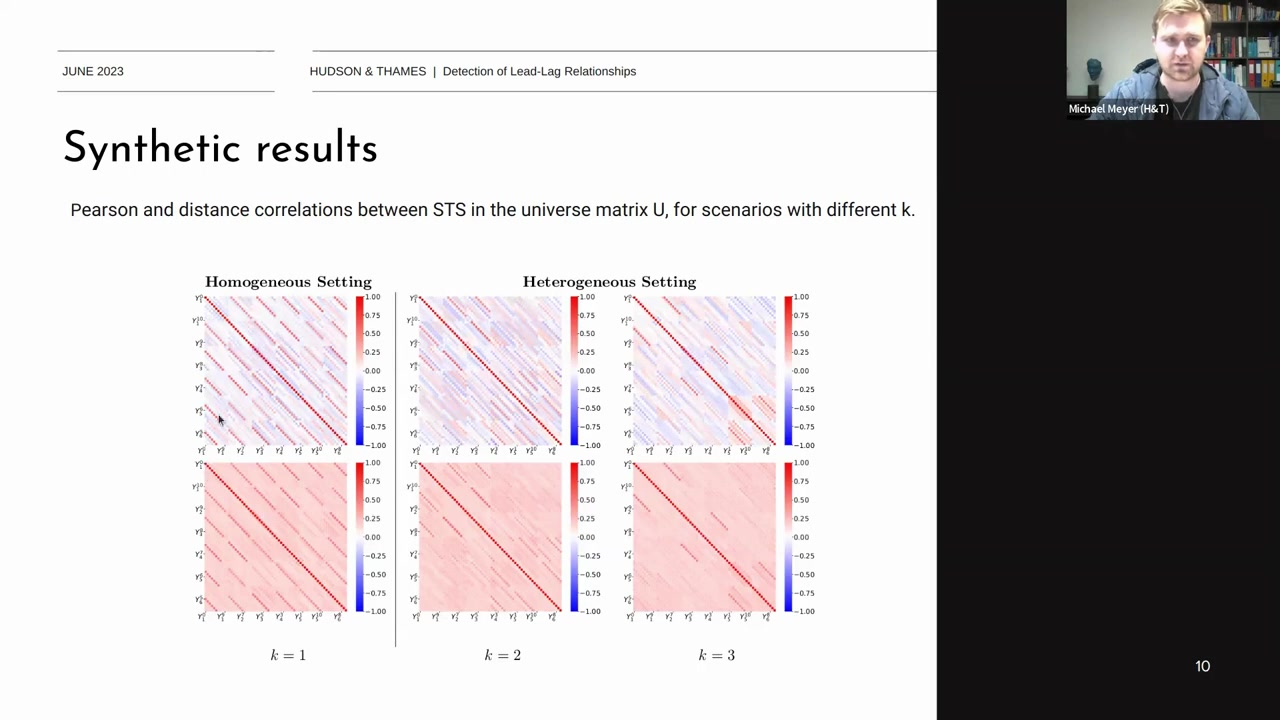
Homogeneous Setting과 Heterogeneous Setting에서 각각 다른 \(k\) 값을 사용하여 STS의 상관 관계 매트릭스를 구성합니다.
- Homogeneous Setting:
- 각 시계열의 시차별 상관 관계를 보여줍니다.
- 예를 들어, 시계열 1의 시차 1은 동일한 시계열 1을 시차 1만큼 이동시킨 것입니다.
- 이러한 방식으로, 시계열 1의 시차 1과 시계열 1의 시차 2 간에는 완벽한 상관 관계가 나타납니다.
- 시계열 2도 마찬가지로 시차별로 이동시키면서 상관 관계를 계산합니다.
- Heterogeneous Setting:
-
- 각 시계열의 상관 관계가 조금 더 복잡해집니다.
- 예를 들어, 시계열 1과 시계열 2의 상관 관계를 계산할 때, 시계열 1을 10번 시프트하고, 시계열 2를 9번 시프트하는 방식입니다.
- 이 설정에서 각 시계열 간의 상관 관계는 보다 다양하게 나타납니다.
각 매트릭스는 서로 다른 \(k\) 값을 사용하여 구성된 STS 간의 상관 관계를 나타냅니다. 빨간색은 양의 상관 관계, 파란색은 음의 상관 관계를 나타냅니다. Homogeneous Setting에서는 상관 관계가 대체로 일정하게 나타나지만, Heterogeneous Setting에서는 상관 관계가 더욱 다양하게 나타납니다.
Pearson Correlation 과 Distance Correlation:
- Pearson 상관 계수는 시계열 간의 선형 상관 관계를 측정합니다. 매트릭스의 대각선은 항상 1로 나타나며, 이는 동일한 시계열의 상관 관계가 완벽하기 때문입니다.
- Distance 상관 계수는 비선형 상관 관계를 포함한 보다 일반적인 상관 관계를 측정합니다. Pearson 상관 계수와는 다른 결과를 제공하며, 비선형 관계를 감지할 수 있습니다.
TODO
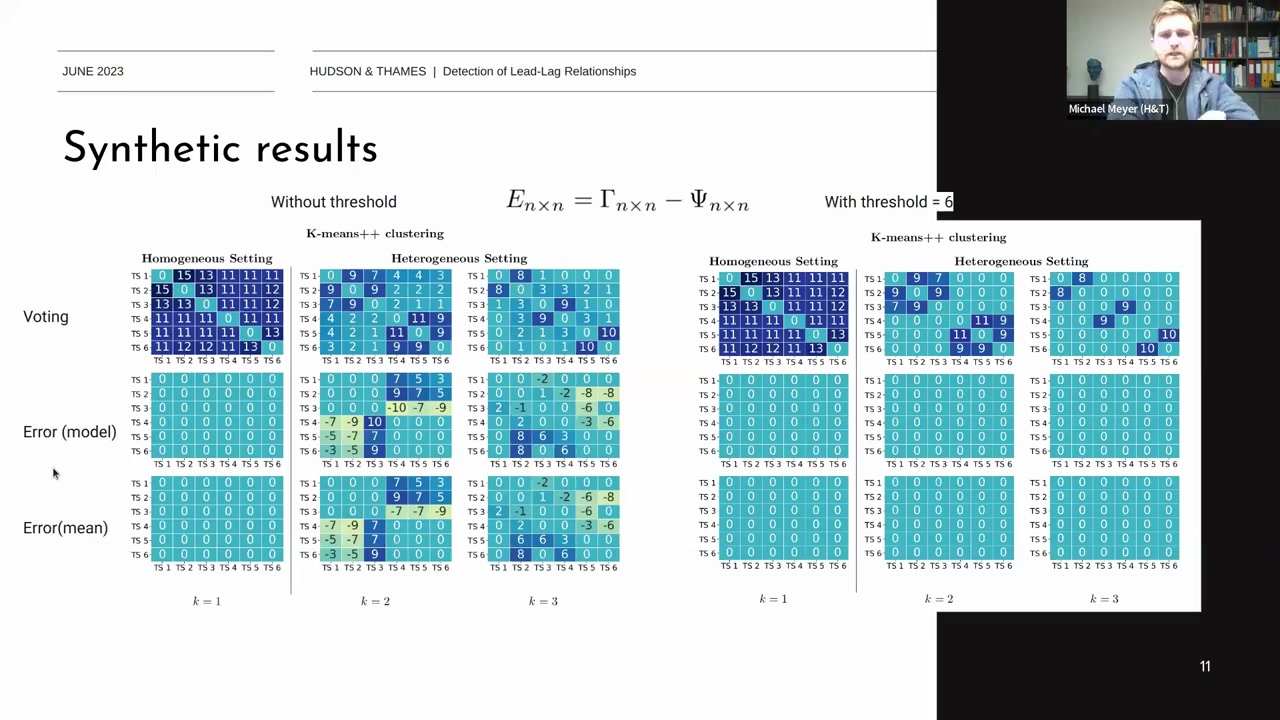
- Empirical Matrix:
- 클러스터링 방법론을 기반으로 계산된 경험적 매트릭스입니다.
- 실제 시차 매트릭스와 비교하여 계산된 결과를 나타냅니다.
- Error Matrix:
- 모드 투표(mode voting)를 사용하여 계산된 오차 매트릭스입니다.
- 시차 매트릭스와의 차이를 나타냅니다.
분석 단계
- Homogeneous Setting:
- k=1,2,3k = 1, 2, 3에서의 결과를 비교합니다.
- 투표 결과, 모드 에러, 평균 에러를 비교하여 성능을 분석합니다.
- 예를 들어, 시계열 1과 시계열 6 간에는 15개의 투표가 있었으며, 시계열 3과 시계열 1 간에는 13개의 투표가 있었습니다.
- 이는 길이가 90인 시계열 데이터를 10번 시프트하여 11개의 시차를 가지게 한 결과입니다.
- Heterogeneous Setting:
- 이질적 설정에서의 결과를 비교합니다.
- 클러스터 내 시차가 일정하지 않아 더 복잡한 패턴을 보입니다.
- 예를 들어, 시계열 1과 시계열 2 간에는 7개의 투표가 있었으며, 시계열 3과 시계열 1 간에는 9개의 투표가 있었습니다.
임계값 설정
- \(theta = 6\)인 경우의 결과를 비교합니다.
- 임계값을 설정하여 적은 수의 투표를 필터링합니다.
- 임계값 설정 전후의 결과를 비교하여 정확성을 확인합니다.
결과 해석
- Homogeneous Setting:
- 임계값을 설정하지 않은 경우와 설정한 경우 모두 시차를 정확하게 파악함.
- 모드 에러와 평균 에러가 모두 0에 가까운 값을 보임.
- Heterogeneous Setting:
- 임계값 설정 전후의 결과에서 일부 오차가 발생.
- 시계열 간의 시차 관계를 정확하게 파악하기 위해 임계값 설정이 중요함을 확인.
결론
- 클러스터링 방법론을 사용하여 시계열 간의 lead-lag 관계를 정확하게 탐지할 수 있음.
- 임계값 설정을 통해 불필요한 시차를 필터링하여 정확성을 높일 수 있음.
- Homogeneous Setting에서는 대부분 정확한 결과를 얻었으나, Heterogeneous Setting에서는 일부 오차가 발생할 수 있음.

Financial Setting
Data
연구에서는 세 가지 데이터 세트를 사용합니다.
- Equity:
- 자산 수: 679개
- 기간: 2000/01/03 - 2020/12/31 (5211일)
- 일별 수익률 데이터
- ETF:
- 자산 수: 14개
- 기간: 2006/04/12 - 2019/07/01 (3324일)
- 일별 수익률 데이터
- Futures:
- 자산 수: 52개
- 기간: 2000/01/05 - 2020/10/16 (5166일)
- 일별 수익률 데이터
설명
- US Equity and ETF Data: 종가 기준으로 조정된 일별 수익률 데이터를 사용합니다.
- Futures: 롤링(rolling) 조정을 통해 연속적인 시계열 데이터를 만듭니다.
- Market Excess Returns: S&P Composite Index를 기준으로 초과 수익률을 계산합니다.
Benchmark
연구에서는 교차 상관 함수(cross-correlation function, CCF)를 벤치마크로 사용합니다.
Cross-Correlation Function (CCF)
여기서 \(I(i, j)\)는 사용자 지정 최대 시차 M에 대해 절대 값의 합으로 정의됩니다.
\(I(i, j) = \sum_{m=1}^{M} |\text{CCF}^{ij}(m)|\)
이 식은 교차 상관 함수의 정규화된 곡선 하단 면적(PSI normalized area under the curve)을 계산합니다. 이를 통해 시차 매트릭스를 생성하고, 클러스터링 방법론에서 생성된 e-lag 관계 매트릭스와 비교하여 사용합니다.
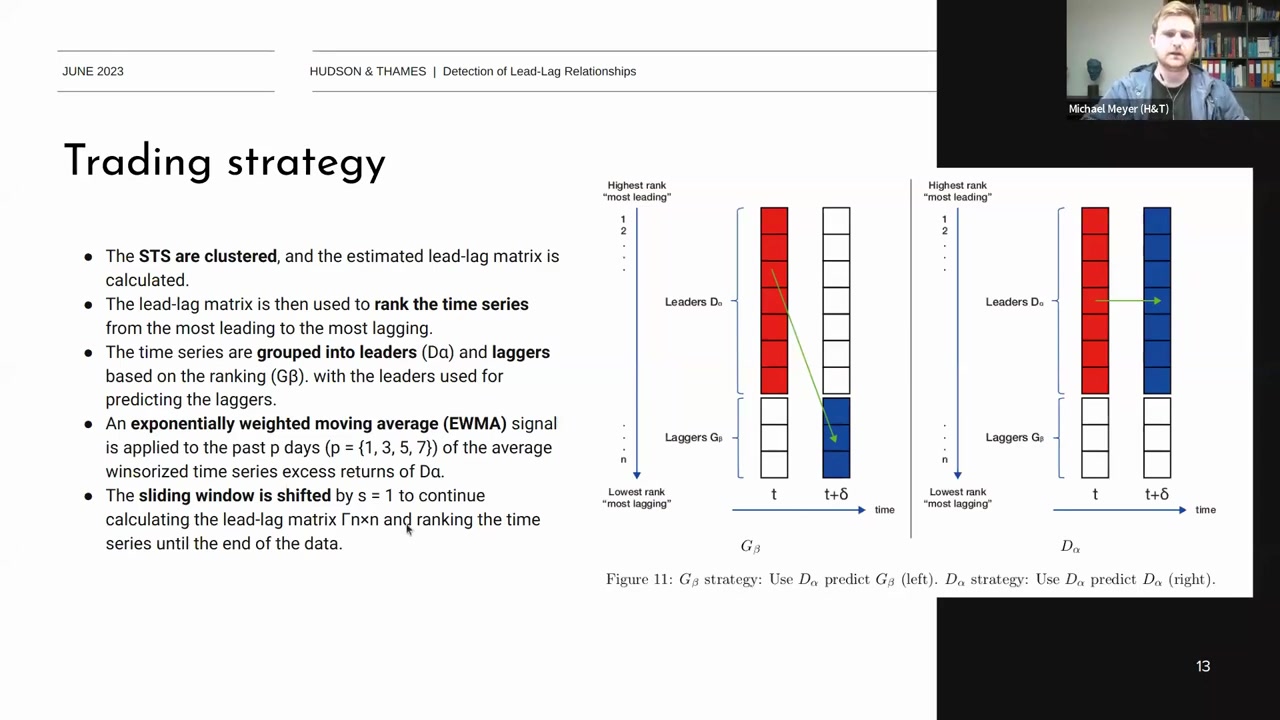
Trading Strategy
- STS Clustering 및 Lead-Lag Relationship 추정:
- STS(Subsequence Time Series)를 클러스터링하여 리드-래그(lead-lag) 관계 매트릭스를 추정합니다.
- K-means++ 또는 Spectral Clustering을 사용하며, 임계값을 설정할 수 있습니다.
- Time Series Ranking:
- 리드-래그 매트릭스를 사용하여 시계열을 리더(Leaders)와 래거(Laggers)로 분류합니다.
- 리더는 가장 앞서는 시계열을 의미하고, 래거는 가장 뒤처지는 시계열을 의미합니다.
- α\alpha와 β\beta를 사용하여 상위 10%, 15%, 25% 등의 리더와 하위 25%, 50% 등의 래거로 분류합니다.
- Exponential Weighted Moving Average (EWMA):
- EWMA 신호를 과거 pp일 (p={1,3,5,7}p = \{1, 3, 5, 7\})의 평균 윈저라이즈드(winsorized) 초과 수익률에 적용합니다.
- 극단적인 수익률을 제거하여 안정된 평균 수익률을 계산합니다.
- Sliding Window:
- 슬라이딩 윈도우는 s=1s = 1만큼 이동하여 리드-래그 매트릭스와 시계열 랭킹을 지속적으로 계산합니다.
- 이를 통해 데이터의 끝까지 지속적으로 계산할 수 있습니다.
Trading Strategy Diagram
- 리더와 래거 그룹화:
- 리더 그룹 (DαD_\alpha)과 래거 그룹 (GβG_\beta)으로 시계열을 그룹화합니다.
- 리더 그룹을 사용하여 래거 그룹을 예측하거나, 리더 그룹을 사용하여 리더 그룹을 예측할 수 있습니다.
- 두 가지 모델:
- 모델 1: DαD_\alpha를 사용하여 GβG_\beta를 예측합니다.
- 왼쪽 다이어그램: 리더 그룹을 사용하여 래거 그룹을 예측.
- 모델 2: DαD_\alpha를 사용하여 다시 DαD_\alpha를 예측합니다.
- 오른쪽 다이어그램: 리더 그룹을 사용하여 리더 그룹을 예측.
- 모델 1: DαD_\alpha를 사용하여 GβG_\beta를 예측합니다.
- 윈저라이즈드(Winsorized) 처리:
- 극단적인 수익률 값을 제거하여 안정적인 수익률을 계산합니다.
- 슬라이딩 윈도우 적용:
- 슬라이딩 윈도우를 사용하여 데이터를 지속적으로 분석하고, 리드-래그 관계를 계산합니다.
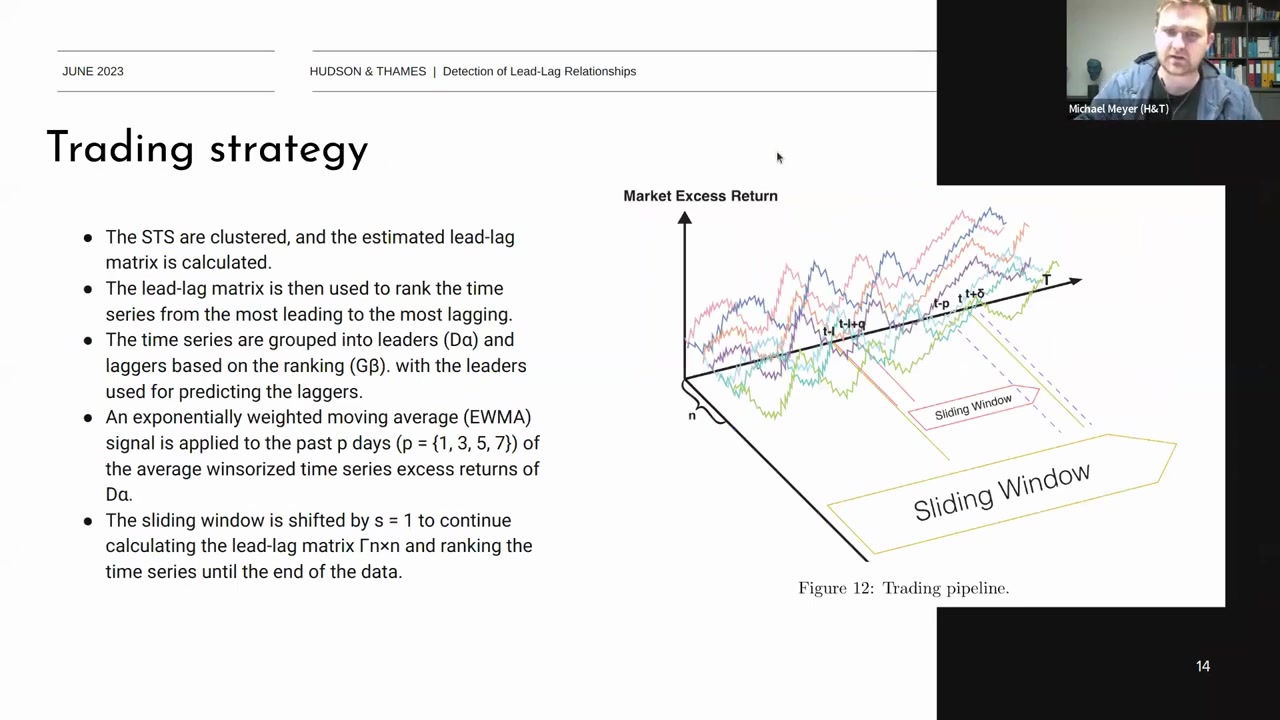
Trading Strategy
- STS Clustering 및 Lead-Lag Relationship 추정:
- STS(Subsequence Time Series)를 클러스터링하여 리드-래그(lead-lag) 관계 매트릭스를 추정합니다.
- K-means++ 또는 Spectral Clustering을 사용하며, 임계값을 설정할 수 있습니다.
- Time Series Ranking:
- 리드-래그 매트릭스를 사용하여 시계열을 리더(Leaders)와 래거(Laggers)로 분류합니다.
- 리더는 가장 앞서는 시계열을 의미하고, 래거는 가장 뒤처지는 시계열을 의미합니다.
- α\alpha와 β\beta를 사용하여 상위 10%, 15%, 25% 등의 리더와 하위 25%, 50% 등의 래거로 분류합니다.
- Exponential Weighted Moving Average (EWMA):
- EWMA 신호를 과거 pp일 (p={1,3,5,7}p = \{1, 3, 5, 7\})의 평균 윈저라이즈드(winsorized) 초과 수익률에 적용합니다.
- 극단적인 수익률을 제거하여 안정된 평균 수익률을 계산합니다.
- Sliding Window:
- 슬라이딩 윈도우는 s=1s = 1만큼 이동하여 리드-래그 매트릭스와 시계열 랭킹을 지속적으로 계산합니다.
- 이를 통해 데이터의 끝까지 지속적으로 계산할 수 있습니다.
Trading Pipeline
- 슬라이딩 윈도우:
- 슬라이딩 윈도우를 사용하여 tt 시점에서 t+δt+\delta 시점까지의 데이터를 분석합니다.
- 과거 pp일 동안의 데이터에서 EWMA 신호를 계산하여 리더와 래거의 초과 수익률을 예측합니다.
- 리더와 래거 그룹화:
- 리더 그룹 (DαD_\alpha)과 래거 그룹 (GβG_\beta)으로 시계열을 그룹화합니다.
- 리더 그룹을 사용하여 래거 그룹을 예측하거나, 리더 그룹을 사용하여 리더 그룹을 예측할 수 있습니다.
- 실행 전략:
- 리더 그룹의 예측 신호를 기반으로 트레이딩 전략을 수립합니다.
- 리더 그룹에서 래거 그룹으로, 또는 리더 그룹에서 리더 그룹으로 예측을 수행하여 수익률을 극대화합니다.
Equity Data Setting:
- 주식 데이터 설정에서의 결과를 분석합니다.
- ETF 및 선물 데이터를 포함한 다른 자산 클래스에서도 테스트를 진행하였으나, 일부 자산 클래스에서는 개선되지 않았음을 언급합니다.
- 소규모 자산 클래스에서는 결과가 미미할 수 있습니다.
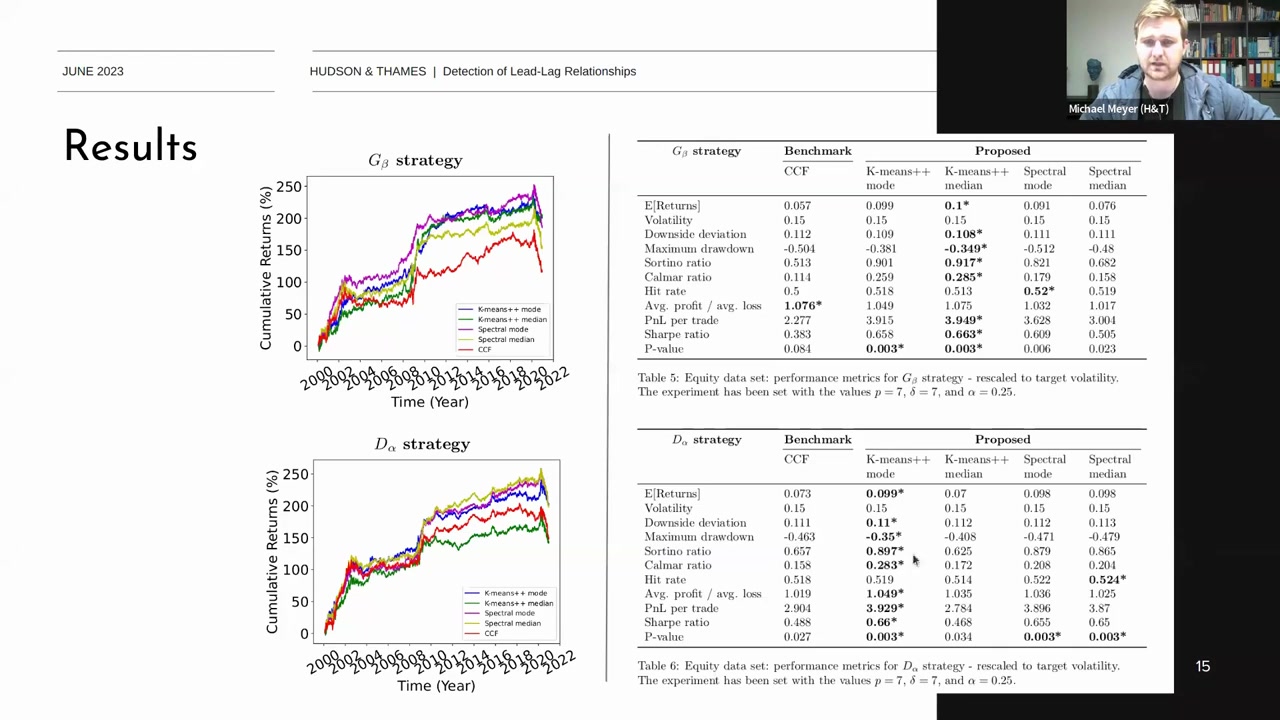
Gβ_\beta Strategy와 Dα_\alpha Strategy의 성과 비교
1. Gβ_\beta Strategy:
- Cumulative Returns: K-means++ (mode), K-means++ (median), Spectral (mode), Spectral (median), 그리고 CCF 방법을 사용하여 수익률을 비교합니다.
- 성과 지표:
- Expected Returns (E[Returns]): K-means++ (median) 방법이 0.1로 가장 높은 수익률을 기록.
- Volatility: 모든 방법에서 0.15로 동일하게 조정.
- Downside Deviation: K-means++ (median)이 가장 낮은 값을 기록.
- Maximum Drawdown: Spectral (mode)이 가장 낮은 값을 기록.
- Sortino Ratio, Calmar Ratio, Hit Rate: K-means++ (median)이 다른 방법보다 우수한 성과를 보임.
- Avg. Profit / Avg. Loss: K-means++ (median)이 1.076으로 가장 높은 값을 기록.
- PnL per Trade: K-means++ (median)이 가장 높은 값을 기록.
- Sharpe Ratio: K-means++ (median)이 0.663으로 가장 높은 값을 기록.
- P-value: K-means++ (median)이 0.003으로 유의미한 성과를 보임.
2. Dα_\alpha Strategy:
- Cumulative Returns: K-means++ (mode), K-means++ (median), Spectral (mode), Spectral (median), 그리고 CCF 방법을 사용하여 수익률을 비교합니다.
- 성과 지표:
- Expected Returns (E[Returns]): K-means++ (mode)이 0.099로 가장 높은 수익률을 기록.
- Volatility: 모든 방법에서 0.15로 동일하게 조정.
- Downside Deviation: K-means++ (median)이 가장 낮은 값을 기록.
- Maximum Drawdown: Spectral (mode)이 가장 낮은 값을 기록.
- Sortino Ratio, Calmar Ratio, Hit Rate: K-means++ (median)이 다른 방법보다 우수한 성과를 보임.
- Avg. Profit / Avg. Loss: K-means++ (median)이 1.049로 가장 높은 값을 기록.
- PnL per Trade: K-means++ (mode)이 가장 높은 값을 기록.
- Sharpe Ratio: K-means++ (mode)이 0.657으로 가장 높은 값을 기록.
- P-value: K-means++ (median)이 0.003으로 유의미한 성과를 보임.
결론
- Gβ_\beta Strategy와 Dα_\alpha Strategy의 비교에서 K-means++ (median) 방법이 대부분의 성과 지표에서 우수한 결과를 보였습니다.
- CCF 방법은 상대적으로 낮은 성과를 보였습니다.
- 특정 시점에서의 큰 손실(drawdown)은 일부 방법에서 우려되는 점으로 나타났습니다.
요약
- K-means++ 클러스터링 방법이 리드-래그 관계를 탐지하고 트레이딩 전략을 수립하는 데 있어서 더 높은 성과를 보였습니다.
- Spectral 클러스터링 방법은 일부 지표에서 더 낮은 손실을 기록하기도 했지만, 전반적으로 K-means++ 방법보다는 낮은 성과를 보였습니다.
- 트레이딩 전략의 적용에서 리드-래그 관계를 기반으로 한 접근 방식이 효과적일 수 있음을 시사합니다.
'HudsonThames > ReadingGroup' 카테고리의 다른 글
| [HudsonThames 리딩그룹] Lead-Lag Detection and Network Clustering (1) (1) | 2024.06.29 |
|---|---|
| [HudsonThames 리딩그룹] Robust Detection of Lead-Lag Relationships in Lagged Multi-Factor Models (2) - 구현 (0) | 2024.06.29 |